柯里化是什么
基本概念
前端中的柯里化(Currying)是一个源自函数式编程的概念。
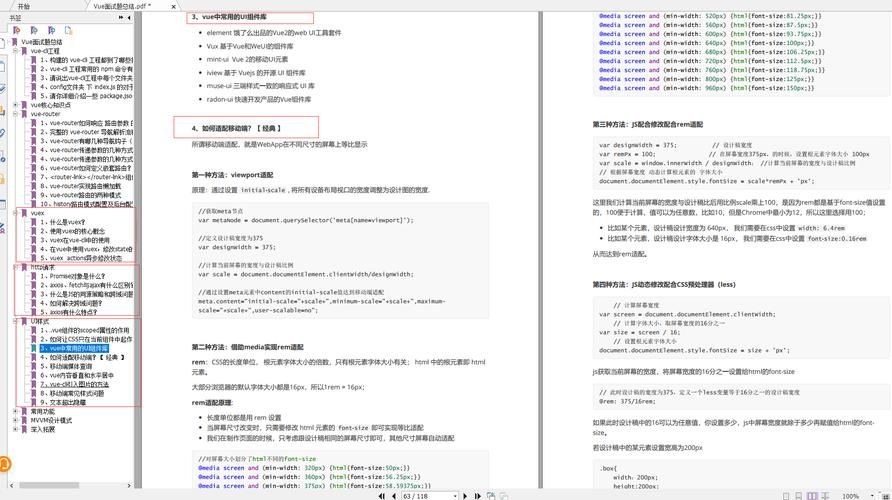
函数式编程,也叫面向函数编程,之后写一篇 React 的函数式编程思想相关的文章
它指的是将原本接受多个参数的函数转换成一系列接受单个参数的函数链的过程。
注意,这里提到了,单个参数!这是个重点,后面要考!
比如对于一个add函数,它原来长这样:
javascript">function add(x, y) {
return x + y;
}
将其柯里化之后就变成了:
function curryAdd(x) {
return function(y) {
return x + y;
};
}
const res = curryAdd(2)(3);
console.log(res); // 输出5
偏函数
偏函数是一个容易与柯里化混淆的概念,它和柯里化的区别是:
柯里化严格要求每次只能传递一个参数,而偏函数则是可以传递任意参数。
也就是:
add(1)(2)(3) // ✅正宗柯里化
add(1)(2, 3)(4) // ❌ 假的柯里化,实际上是偏函数
所以严格来说,柯里化函数是一种特殊的偏函数。
我们前端圈子内,平时口头上都叫柯里化,不需要严格区分。
知晓这个小知识,面试倒是可以多点谈资。
柯里化有什么用
还记得之前面试某个大厂的时候,反问面试官柯里化有什么用,他也愣住了,有点尴尬。
所以我觉得做开发,无论是学什么技术理论,都要结合实际场景,落到实处,不然就只是纸上谈兵。
场景1:拆分计算
试想一下这个场景:这里有个获取用户数据的函数,该函数需要一个ID和dataKey作为参数。
先来看看不使用柯里化的方式
// 先获取userId,然后获取dataKey
getUserId().then(userId => {
getDataKey().then(dataKey => {
// 注意看这里:要两个参数都获取到了后才能开始计算
processUserInfo(userId, dataKey);
});
});
在这个非柯里化的实现中,我们必须等到dataKey准备好后,才开始根据userId发起获取用户数据的请求。这意味着,在获取dataKey的等待时间内,我们无法利用这段时间来获取用户数据,导致整体执行时间较长。
为了提高效率,我们可以使用柯里化技术
getUserId().then(userId => {
// 假设这里把 processUserInfo 柯里化了
const next = processUserInfo(userId, dataKey);
getDataKey().then(dataKey => {
next(dataKey)
});
可以看到,processUserInfo函数柯里化后,返回的是一个新的函数next。
并且,它们就像是在一场接力赛中,每次执行都可以只完成部分计算,剩下的部分可以交给下一个函数接力。
这样做的好处是,可以先完成部分计算,先实现部分效果(比如先更新部分页面等等),再逐步实现后续效果,整体会相对比较流畅。
就问柯里化厉不厉害吧!
场景2:工厂函数
在KOA框架的中间件工厂函数中,柯里化用的也是比较多。
// 中间件工厂函数
function createMiddlewareFactory(param) {
return function middleware(next) {
return async function(ctx, nextInner) {
// ...
await next(ctx, nextInner);
// ...
};
};
}
app.use(createMiddlewareFactory(param1)());
app.use(createMiddlewareFactory(param2)());
这里用工厂模式的发挥的作用是:
-
可以通过不同参数(
param1和param2)来创建结构类似但不同的中间件,这样就不需要写多个创建函数了。 -
而且即使传递相同的参数,每次调用函数都能返回一个新的实例,不会是原来的引用,保证了每个中间件都是独立的。
另外,我们再看看KOA中间件的回调函数的朴素写法,它是这样的:
app.use(async (ctx, nextInner) => {
await next(ctx, nextInner);
// 想想 next 函数从哪来的呢
});
再多结合上面的中间件工厂函数看看,我们就可以感知到,柯里化在其中发挥的作用是:
-
格式化了参数(
ctx和nextInner)。 -
通过闭包传递了上下文(
next)。
如何实现柯里化
虽然说上面已经给出了很多案例代码,但是都还是没有总结沉淀出一套方法论,不能做到一针见血地体现其实现方法。
这里给出几个版本,针对不同基础的群体。
基础学习版:新人入门
柯里化的精髓就是,闭包+判断参数个数。
闭包就是函数返回函数,很好实现。
至于如何获取到参数个数,有两种方法:
- 第一是
arguments对象,这是一个可以直接在函数上下文中获取到的对象,是一个伪数组(JS早期设计缺陷的产物之一),代表实际传入的参数。
function say() {
console.log(arguments[0])
// 因为是伪数组,要用数组API的话得先转成真数组
// 即 const arr = Array.from(arguments)
}
- 第二是
Function.prototype.length,也就是一个函数的length属性其实就是它声明的参数数量。
function say() {
console.log(say.length) // 0,因为没有声明参数
}
一般而言,我们更习惯用第二种(毕竟第一种都涉及早期JS黑历史,用着感觉也别扭),代码如下:
// 定义一个柯里化函数
function curry(func) {
// ...args代表任意数量的参数,args是一个数组
return function curried(...args) {
// 实际传参数量 >= 声明参数数量
if (args.length >= func.length) {
// 正常执行
return func(...args);
} else {
return function(...moreArgs) {
// concat拼接一下参数,凑齐了再执行
return curried(...args.concat(moreArgs));
};
}
};
}
// 下面是使用案例:
function add(...args) {
return args.reduce((total, num) => total + num, 0);
}
console.log(sum(1)(2)(3)(4)); // 输出10,相当于调用 add(1, 2, 3, 4)
console.log(sum(1, 2)(3, 4)); // 输出10,同样相当于调用 add(1, 2, 3, 4)
极简精华版:一行代码
原理和上面的一样,但主打一个浓缩和精简,并且通用支持任意形式的传参,足够应付面试场景:
const curry = (fn, ...args) =>
args.length >= fn.length ? fn(...args) : (...args) => curry(fn, ...args, ..._args);
// 用法示例:
const add = (...nums) => {
return nums.reduce((sum, num) => sum + num, 0);
};
const curriedAdd = curry(add);
console.log(curriedAdd(1, 2, 3, 4, 5));
console.log(curriedAdd(1)(2)(3));
console.log(curriedAdd(1)(2)(3)(4)(5)); // 输出:15
魔改升级版:闭包乱炖
还有一种场景的面试场景,就是不只是要单纯地实现柯里化,还要结合更多需求。
考灵活运用也合理,不然手写这些个柯里化又有啥实际意义呢
通常都是围绕着闭包的用法来考,举个简单但是足够经典的例子:
curriedAdd(1)(2)(3)
// 期望它每次调用的时候都能进行输出当前的总和
// 也就是输出三次,分别是:1 3 6
实现的代码如下:
function curry(initial = 0) {
let currentSum = initial;
const add = (...args) => {
return args.reduce((total, num) => total + num, 0);
}
return function(...args) {
currentSum += add(...args);
console.log(currentSum); // 输出当前的总和
// 如果没有参数传入,返回最终结果;否则返回新的柯里化函数
return args.length === 0 ? currentSum : curry(currentSum);
};
}
// 创建一个柯里化求和并打印中间结果的函数
const curriedAddAndLog = curry();
// 使用示例
curriedAddAndLog(1)(2)(3); // 分别输出:1、3、6
curriedAddAndLog(1)(2, 3)(4) // 1、6、10
如果你不太理解闭包的原理,诸如调用栈、作用域链、outer指针等等概念,也不太了解闭包的实际应用,但又想快速应付面试,那你可以简单地把闭包题目总结为:
- 函数套函数。
- 两层函数的“夹缝”之间,可以放一些变量,这些变量对于下面那层函数来说,就像是全局变量一般,可以随时用。
按部就班地实现上述两步,再把题目的具体要求往里面一套,一切都变得非常简单而美妙了。

